√無料でダウンロード！ (a-b)^3 proof 215304-A^3+b^3+c^3-3abc proof

P(A∪B) = P(A)P(B)−P(A∩B) Proof There is A∪(B∩Ac) = (A∪B)∩(A∪Ac) = A∪B, which is to say that A∪B can be expressed as the union of two disjoint sets Therefore, according to axiom 3, there is P(A∪B) = P(A)P(B ∩Ac) But B = B ∩ (A ∪ Ac) = (B ∩ A) ∪ (B ∩ Ac) is also the union of two disjoint sets, so there is alsoDon't forget to like, comment, and subscribe!!!Subscribe for new videos wwwyoutubecom/c/MrSalMathShare this video https//youtube/IoqYK6YlyBIThe problemRegister for FREE at http//deltastepcom or download our mobile app https//bitly/3akrBoz to get all learning resources as per ICSE, CBSE, IB, Cambridge &

Www Ddtwo Org Cms Lib Sc Centricity Domain 1986 Distance learning notes on congruent triangles Pdf

A^3+b^3+c^3-3abc proof

A^3+b^3+c^3-3abc proof-`(ab)^3 = a^3 3a^2*b 3ab^2 b^3` You should factor out 3ab in the group `3a^2*b 3ab^2` such that `(ab)^3 = a^3 b^3 3ab(ab)`For all positive integers a and b, LCM(a,b) is unique Pf (We shall omit the proof of the existence of the LCM and just show it's uniqueness, assuming that it exists) Let a and b be positive integers Suppose m 1 and m 2 are two LCM's for a and b Since m 1 is an LCM and m 2

Proof Without Words Payment Proof

Identity 3 Let A, B and C be sets Show that (A−B)−C = A−(B ∪C) Proof (A−B)−C = (A∩)−C set difference = (A∩)∩Cc set difference = A∩( ∩Cc) associative = A∩(B ∪C)c de Morgan's = A−(B ∪C) set difference Proof Let x ∈ (A − B) − C Then x ∈ (A − B) and x 6∈C by definition of set differenceA )(B )C) (A and B) )C conditional proof In a course that discusses mathematical logic, one uses truth tables to prove the above tautologies 2 Sets A set is a collection of objects, which are called elements or members of the set Two sets are equal when they have the same elementsProve ABC =(AB)(AC) jaisonshereen asked on Puzzles / Riddles;

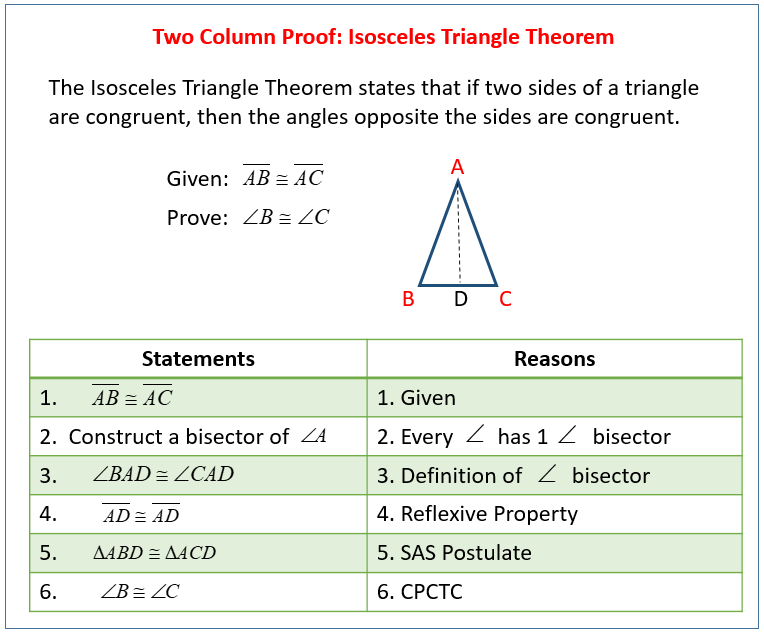
Transitive If ∠ ≅∠A B and ,∠ ≅∠B C then ∠ ≅∠A C Notes Writing a TwoColumn Proof In a proof, you make one statement at a time until you reach the conclusion Because you make statements based on facts, you are using deductive reasoning Usually the first statementandreason pair you write is given informationThe expansion of a minus b whole squared algebraic identity can be derived in algebraic form by the geometrical approach The concept of areas of geometrical shapes such as squares and rectangles are used for proving the a minus b whole square formula in algebraic form114 (e) Prove that A∩B and A\B are disjoint, and that A = (A∩B)∪ (A\B) Proof For the first part we have to prove that (A ∩ B) ∩ (A \ B) = ∅ Let x ∈ (A ∩ B) ∩ (A \ B) Then x ∈ A ∩ B and x ∈ A \ B, so x ∈ A and x ∈ B, and x ∈ A and x /∈ B In particular, this implies x ∈ B and x /∈ B, which is a

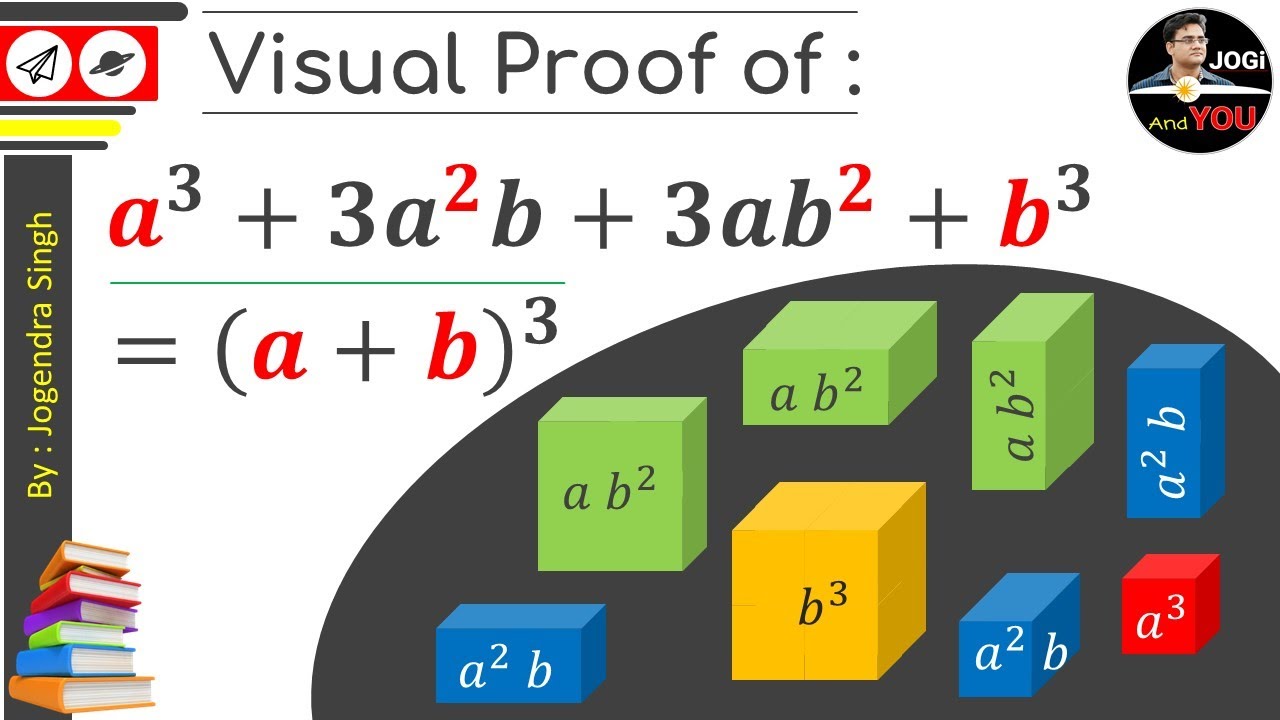
Summary (AB)^3 If you have any issues in the (AB)^3 formulas, please let me know through social media and mail A Plus B Whole Cube is most important algebra maths formulas for class 6 to 13Proof by induction applied to a geometric series Alisoncom Proof of the Sum of Geometric Series Project Maths Site Further proof by induction – Multiples of 3 Alisoncom Factorisation results such as 3 is a factor of 4n–1 Proj Maths Site 1 Proj Maths SIte 2 Prove De Moivre's Theorem Further proof by induction – Factorials andSince (ab)^3= a^3b^33ab(ab) =>(ab)^33ab(ab)=a^3b^3 =>(ab)((ab)^23ab)=a^3b^3 =>(ab)(a^2b^2ab)=(ab)^3

Give Me The Proof Of A 3 B 3 Mathematics Topperlearning Com Zcc4adww

Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo

Let me help you with this formula in detail (a b c)³ = a³ b³ c³ 3 (a b) (b c) (a c) Proof (a b c)³ = a³ b³ c³ 3 (a b) (b c) (a c)Any integer can be factored into prime numbers, its 'divisors' for example, 60 = 5 x 3 x 2 x 2 The conjecture roughly states that if a lot of small primes divide two numbers a and b , thenFor all integers \(a\) and \(b\text{,}\) if \(a\) and \(b\) are even, then \(ab\) is even There are numbers \(a\) and \(b\) such that \(ab\) is even but \(a\) and \(b\) are not both even False For example, \(a = 3\) and \(b = 5\text{}\) \(ab = 8\text{,}\) but neither \(a\) nor \(b\) are even

Cubic Formula Proof A B 3 A3 3a2b 3ab2 Proof Of A B 3 Expand A B 3 A B Whole Cube Youtube

Two Column Proofs Video Lessons Examples Solutions

Multiplying the binomial a b by itself three times is the mathematical meaning of cube of the binomial a b So, the a plus b whole cube can be expressed in product form by multiplying three same binomials ( a b) 3 = ( a b) × ( a b) × ( a b) Multiplying three same binomials is a special case in mathematics2 2 Problem 9 of worksheet 3 Proposition 9 For any a;b 2Z, it follows that (a b)3 a3 b3(mod3) Proof Suppose a;b 2Z Thus, there is an integer x such that x = a2b ab2Hence 3x = 3a2b 3ab2 = (a b)3 a3 b3 It follows that 3j(a b)3 3a 3 b3Therefore, (a b) a3 b (mod3) ProofDavneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 9 years He provides courses for Maths and Science at Teachoo

A B 3 A 3 3a 2b 3ab 2 B 3 Proof Algebraic Proofs Mathematical Proofs Binomial Expansions Algebra Proofs Art Mathematics

Proof Of Cos A B Cosacosb Sinasinb Sum And Difference Identities For Pdf

Proof (ab)• (a2abb2) = a3a2bab2ba2b2ab3 = a3 (a2bba2) (ab2b2a)b3 = a300b3 = a3b3 Check b3 is the cube of b1 Check a3 is the cube of a1 Factorization is (b a) • (b2 ba a2)So, Area of square of length (ab) = (ab) 2 = (i) (ii) (iii) (iv) Therefore (ab) 2 = a 2 ba ba b 2 ie (ab) 2 = a 2 2ab b 2 Hence Proved This simple formula is also used in proving The Pythagoras Theorem Pythagoras Theorem is one of the first proof in MathematicsThis is basically the proof of 0a=0 hidden within this other proof $\endgroup$ – Sebastian Garrido Dec 14 '13 at 1544 $\begingroup$ @SebastianGarrido that's right I have now colored that part in blue and hopefully this make everyone easier to see $\endgroup$ – achille hui Dec 14 '13 at 1950

Solved Use A Proof By Contradiction To Prove Please Show Chegg Com

Algebra Sleuth Proof That 1 2 Activity Education Com

A(BC) = (AB)C Proof If A, B and C are three variables, then the grouping of 3 variables with 2 variables in each set will be of 3 types, such as (A B), (B C) and(C A) According to associative law (A B C) = (A B) C = A (B C) = B (C A) We know that, A AB = A (according to Absorption law)Note the quality q(a, b, c) of the triple (a, b, c) is defined above Refined forms, generalizations and related statements The abc conjecture is an integer analogue of the Mason–Stothers theorem for polynomials A strengthening, proposed by Baker (1998), states that in the abc conjecture one can replace rad(abc) by ε −ω rad(abc), where ω is the total number of distinct primesProof for the Change of Base Rule Proof Step 1 Let x = log a b Step 2 Write in exponent form a x = b Step 3 Take log c of both sides and evaluate log c a x = log c b xlog c a = log c b Videos Proof of the logarithm properties Proof of Product Rule log A log B = log AB Show Stepbystep Solutions

Www Montgomery Kyschools Us Userfiles 1864 Classes Day 2 parallelogram proofs ws key Pdf

Solved 2 10 Marks Let A And B Be Sets Prove That A Chegg Com

A )B Equivalence A if and only if B A ,B Here are some examples of conjunction, disjunction and negation x > 1 and x < 3 This is true when x is in the open interval (1;3) x > 1 or x < 3 This is true for all real numbers x(x > 1) This is the same as x 1 Here are two logical statements that are true x > 4 )x > 2 x2 = 1 ,(x = 1 or x = 1)Using algebra and a little deception, Mr John Hush proves (or does he?) that 1 = 2 to a class of amazed calculus studentsIn mathematics, Weitzenböck's inequality, named after Roland Weitzenböck, states that for a triangle of side lengths , , , and area , the following inequality holds ≥ Equality occurs if and only if the triangle is equilateral Pedoe's inequality is a generalization of Weitzenböck's inequality The Hadwiger–Finsler inequality is a strengthened version of Weitzenböck's inequality

Solved Complete The Proof Given Ef 10 3 Ac Eg A B Prove Fg 10 E F G Statements Reasons 14 Ac Ab 15 Ab 10 3 16 Substit Course Hero

File Difference Of Squares And Cubes Visual Proof Svg Wikimedia Commons

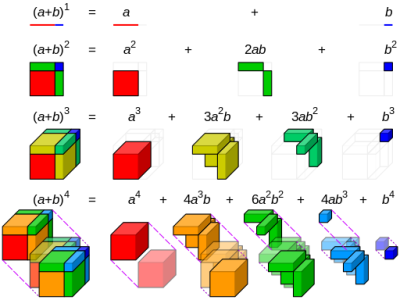
J) a rational number means that it has the form a/b where a,b ∈ Z and b 6= 0 3 A theorem can by symbolized in logical notation as (P ∨ Q) ∧ R ⇒ S ∧ ∼ W Outline the framework you would use (assumptions and goals) for the following You are expected to work any negations through as much as possible a) Direct proof ASSUMPTION (P ∨ Q) ∧ RThus by de nition (a b)3 = a3 3a2b 3ab b3 Proof Let a;b;2Z Then (ab)3 = a3 3a2b3ab2 b 3 Hence (ab)3 (a3 b3) = a 3a2b3ab2 b3 a3 b3 This is equivalent to 3a2b 3ab 2= 3(a2b ab2) We see that a2b ab is an integer, thus by the de nition of divisibility which states that for any integer x;y, we say that x divides y if there is an integer c such that y = xc, 3 j(a b)3 (a3 b3)1 (a b)2 = a2 2ab b2 2 (a b)2 = a2 2ab b2 3 (a b)3 = a3 b3 3ab(a b) 4 (a b)3 = a3 b3 3ab(a b) 5 (a b c)2 = a2 b2 c2 2ab2bc

Simple Proof Of A B A 3a B 3ab B A B 3ab A B And A B A 3a B 3ab B A B 3ab A B Youtube

Www Ddtwo Org Cms Lib Sc Centricity Domain 1986 Distance learning notes on congruent triangles Pdf

Here is animated view of formula Cube of a sum =(ab)³=a³3a²b3ab²b³ You can see both cubes and the six rectangular parallelepipeds in 3Dview Cube of a difference The formula is (ab)³=a³3a²b3ab²b³ You convert it to (ab)³=a³3ab(ab)bLearn how to derive the expansion of a plus b whole cube formula in algebraic approach by the special product of three same binomials mathematicsLemma 33 Let a,b be integers with a > b > 0 Then gcd (a,b) =gcd(b,a−b) Proof Let gcd(a,b) = d and gcd(a−b,b) = e da and db so d(a−b) (by 31) Hence d ≤ e (as e is the greatest common divisor of b and a−b) Also e(a−b) and eb so ea and hence e ≤ d (as d is the greatest common divisor of a and b) Thus d = e

Fermat S Library Visual Proof Of Cubic Binomial A B A 3ab 3ba B

Solved 3 Prove The Following Statement For Every Set A Chegg Com

6 a2 −b2 =(ab)(a−b) 7 a3 −b3 =(a−b)(a2 ab b2) 8 a3 b3 =(ab)(a2 −ab b2) 9 a n−bn=(a−b)(an−1 a −2b an−3b2 bn−1) 10 an= aaantimes 11 ama n= am 12 am an = am−nif m>n =1 ifm=n = 1 an−m if mSo, Area of square of length (ab) = (ab) 2 = (i) (ii) (iii) (iv) Therefore (ab) 2 = a 2 ba ba b 2 ie (ab) 2 = a 2 2ab b 2 Hence Proved This simple formula is also used in proving The Pythagoras Theorem Pythagoras Theorem is one of the first proof in Mathematics2 PROOFS (1) A 1 is invertible with inverse A (2) AB is invertible with inverse B 1A (3) AT is invertible with inverse (A 1)T Proof — Part (1) Since A is invertible, it follows that 9A 1 such that AA 1 = A 1A= I n However, by definition this immediately implies that A 1 is invertible with inverse A Part (2) Since A,B are invertible, it follows that 9A 1;B 1such that AA = A 1A=

Http Math Hws Edu Eck Math135 F19 5 6 Answers Pdf

New Page 1

Cube Formulas (a b) 3 = a 3 b 3 3ab (a b) (a − b) 3 = a 3 b 3 3ab (a b) a 3 − b 3 = (a − b) (a 2 b 2 ab) a 3 b 3 = (a b) (a 2 b 2 − ab) (a b c) 3 = a 3 b 3 c 3 3 (a b) (b c) (c a) a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) If (a b c) = 0,27 Comments 1 Solution 21,561 Views 1 Endorsement Last Modified prove ABC =(AB)(AC) Comment Premium Content You need a subscription to comment Start Free Trial Watch QuestionBy definition of ( ) symbol (a) means additive inverse of (a) and (b) means additive inverse of (b) As a * 0 = 0 by multiplicative property of zero a * {b (b)} = 0 using additive inverse a*b a(b) = 0 multiplicative associative pro

A B 3 Geometric Proof

A B 3 I E A Plus B Cube Formula Proof Ntse Algebraic Formulas Identity Geometrically Youtube

Proof Formula \((abc)^3 = \\a^3 b^3 c^3 6abc \\ 3ab (ab) 3ac (ac) 3bc (bc) \) Summary (abc)^3 If you have any issues in the (abc)^3 formulas, please let me know through social media and mailProof Formula \(=> a^3 b^3 = (ab) (a^2 b^2 – ab) \) Verify \( a^3 b^3 \) Formula Need to verify \( a^3 b^3 \) formula is right or wrong put the value of a =2 and b=3 put the value of a and b in the LHS \( => a^3 b^3 = 2^3 3^3 \) \( = > a^3 b^3 = 8 27 = 35 \) put the value of a and b in the RHS \(=> (ab) (a^2 b^2 – ab) \) \(=> (23) (2^2 3^2 2 \times 3) \) \(=> (5) (4 9 – 6) \) \(=> (5) (7) = 35 \) Therefore \( LHS = RHS \) LHR = left hand side, RHS = right hand2 PROOFS (1) A 1 is invertible with inverse A (2) AB is invertible with inverse B 1A (3) AT is invertible with inverse (A 1)T Proof — Part (1) Since A is invertible, it follows that 9A 1 such that AA 1 = A 1A= I n However, by definition this immediately implies that A 1 is invertible with inverse A Part (2) Since A,B are invertible, it follows that 9A 1;B 1such that AA = A 1A=

What Is The Correct Formula Of Math A B 3 Math Quora

Answered What Is The Reason For Statement 3 Bartleby

In summary, we have shown that if \(A \times C = B \times C\), then \(A = B\) This completes the proof Now we'll look at another way that set operations are similar to operations on numbers From algebra you are familiar with the distributive property \(a \cdot (bc) = a \cdot ba \cdot c\) Replace the numbers a,b,c with sets A, B, C, and= (b^3)(2n^3 3n^2 n)/(6n^3) The area from 0 to a, A_2, can be approximated as a/n • (Σ (ai/n)^2 i = 1 to n) = (a^3)(2n^3 3n^2 n)/(6n^3) Then an approximation of the area from a to b is A_1 A_2 = (b^3 a^3)(2n^3 3n^2 n)/(6n^3) The exact area, then, is lim_{n→∞} (b^3 a^3)(2n^3 3n^2 n)/(6n^3) = 2(b^3 a^3)/6 = (b^3 a^3)/3Solution This proceeds as Given polynomial (8a 3 27b 3 125c 3 – 90abc) can be written as (2a) 3 (3b) 3 (5c) 3 – 3 (2a) (3b) (5c) And this represents identity a 3 b 3 c 3 3abc = (a b c) (a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c

Solution Given Db Is Not Congruent To Ac To Prove Ab And Cd Do Not Bisect Each Other Drawing 400 400 6 6 6 6 Line 4 4 4 5 Line 5 4 5 4 Line 4 4 5 4 Line 5 4 4 5

A B 3 Proof

Identity VII (a − b) 3 = a 3 b 3 3ab (a b) Check Algebra Formulas for full list of formulas Lets take an example Identity VI (a b) 3 = a 3 b 3 3ab (a b) (2 3) 3 = 2 3 3 3 3 (2) (3) (2 3) (5) 3 = 8 27 18 × 5 125 = 8 27 90 125 = 125 Identity VII (a − b)3 = a3 b3 3ab (a b)Theorem Let A = {n n = 4k 1 for some k ∈ Z} and B = {n n = 4k −3 for some k ∈ Z} Prove A = B Proof We must show that A ⊆ B and B ⊆ A First, we show that A ⊆ B Let x ∈ A By definition of A, x = 4m1 for some m ∈ Z Letting n = m 1, we check by substitution that 4n − 3 = 4(m 1)− 3 = 4m 4− 3 = 4m 1 = xRecall (Definition 13) that if A and B are sets, then A ⊆ B means that every element of A is also an element of B In other words, it means if a ∈ A, then a ∈ B Therefore to prove that A ⊆ B, we just need to prove that the conditional statement "If a ∈ A, then a ∈ B " is true

The Colored Proof Has Been Translated Into A Colored Two Column Proof Download Scientific Diagram

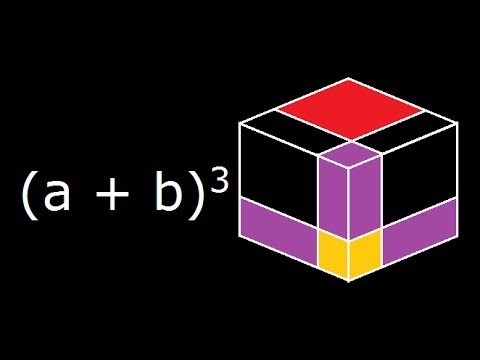
A B 3 A Plus B Cube Algebra Identity Geometrical Explanation And Derivation Youtube

I guess another way of looking at it would be (ab)^3 = a^3 b^3 3(a^2)b 3a(b^2) Remember this formula It is simpler P now, to find the value of a^3 b^3, we move all the other terms to the left which gives us (ab)^3 (3(a^2)b 3a(b= (a b)(a b)(a b) = (a b)(a² ab ab b²) = (a b)(a² 2ab b²) = a³ 2a²b ab² a²b 2ab² b³ = a³ 3a²b 3ab² b³Example Solve 8a 3 27b 3 125c 3 – 90abc Solution This proceeds as Given polynomial (8a 3 27b 3 125c 3 – 90abc) can be written as (2a) 3 (3b) 3 (5c) 3 – 3(2a)(3b)(5c) And this represents identity a 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3

Www Math Ucla Edu Azhou Teaching 19s 131 Hw 02 Sols Pdf

To Prove 3 Left A B 2 B C 2 C A 2 Right 4 Left A D 2 B E 2 C F 2 Right Proof A B 2 A C 2 2 Left A D 2 B D 2 Right M R 3 X 4

Geometry Proofs Wikiversity

A B 3 Geometric Proof

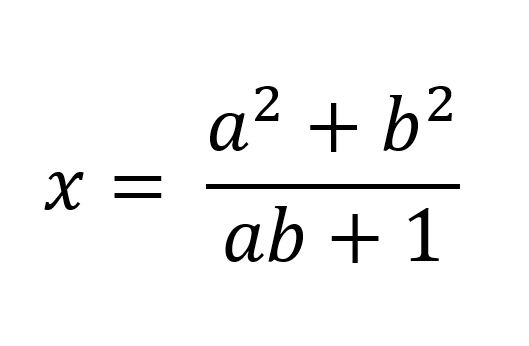
19 Imo Question Six Solving The Hardest Problem On The By Maths And Musings Cantor S Paradise Medium

Match The Reasons With The Statements In The Proof To Prove Ab Dc Given That Ad Is Parallel To Brainly Com

Q Tbn And9gcrswdldblxmiitn Ggstx6knbcgxw3sex0r673zeswoh Igfkvn Usqp Cau

Proof Without Words Payment Proof

Proof Of A B 3 A3 3a2b 3ab2 Proof Of A B 3 Formula Youtube

How To Falsely Prove That Pi Equals 3 7 Steps With Pictures

Illustrations Of Formulas

What Is The Formula Of Math A B 3 Math Quora

Algebraic Identities For Class 8 Formulas And Proofs

Firststep By Rishabh Singla Geometrical Visual Proof Of The Famous Formula A B 2 A 2 B 2 2 A B

Two Column Proofs Given 2x 3 2 3 Prove X 11 6 Statements Ppt Download

Plane Geometry Circles Is This Proof Correct Homeworkhelp

Derivation Of Formula For A B 3

How To Prove The Identiy A3 C3 3abc Math Polynomials Meritnation Com

Www Shsu Edu Kws006 Math History 2 The Greek Age Files 2 Ws Greekage Pdf

What S Wrong With This Proof Let Others Ponder It As Well A

Vector Analysis By Alimkanwalimtinaa Issuu

Plane And Solid Geometry Given Str Line Fb1 Ab And To At B And Plane Mn Con Taining Ab And To Prove Fb Plane Mn Lt Outline Of Proof 1

2

A Minus B Cube Or A Minus B Whole Cube A B 3 Geometric Explanation Derivation Youtube

Http Www Math Cmu Edu Wgunther 241 M14 Hw Hw3soln Pdf

3 2 8 Is Det Ab Det Ba

Proof Of The Formula For A 3 B 3

Inequalities Marathon

4 Complete The Following Activity By Observing The Given Ve Math

Www Tesd Net Cms Lib Pa Centricity Domain 263 Geo h unit 2 proof practice solutions Pdf

Solved Question 1 Given The Following Argument 1 A B C Chegg Com

A B 3 Proof

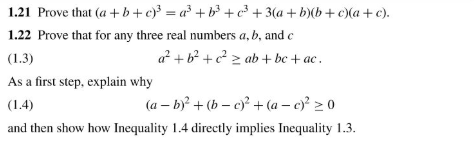
Solved 1 21 Prove That A B C 3 A3 C3 3 A B Chegg Com

Www Studocu Com Row Document E4 B8 8a E6 B5 E4 Ba E9 80 9a E5 E5 Ad B8 E9 Ab 98 E7 Ad E6 95 B0 E5 Ad A6 A Other Eigenvalues Of Ab And Ba View

Http Math Bu Edu People Rpollack Teach 129fall10 129midterm1 Solns Pdf

Solved Mp Q3 Developing Proof Complete The Flow Proof Below Given 21 And 213 Are Supplementary Prove A B 3 21 And 23 Are Supplementary D Alb Course Hero

A B 3 A3 3a2b 3ab2 But Why Math Formula Proof A B 3 And Algebraic Explanation Youtube

Illustrations Of Formulas

2

How Should I Prove A B 3 A 3 3ab A B B 3 Model Or Figure Mathematics Stack Exchange

Exam 2 Questions For Elements Of Geometry And Measurement Math 213 Docsity

Search Q A 5e3 2bb 5e3 Formula Tbm Isch

Prove A Group Is Abelian If Ab 3 A 3b 3 And No Elements Of Order 3 Problems In Mathematics

Misc 4 If A And B Are Symmetric Matrices Prove Ab Ba Is

Example 3 Use Properties Of Equality Ppt Video Online Download

Lesson 5 3 Multiplying Polynomials Objectives Students Will Multiply Any Polynomials Multiply Binomials Using Foil Square A Binomial Multiply The Sum Ppt Download

Binomial Theorem

Help Pleasedrag A Reason To Each Box To Complete The Proof Given Ac Line Segment A D With Points Brainly Com

Algebra Sleuth Proof That 1 2 Activity Education Com

Write The Geometrical Proof Of A B 3 Brainly In

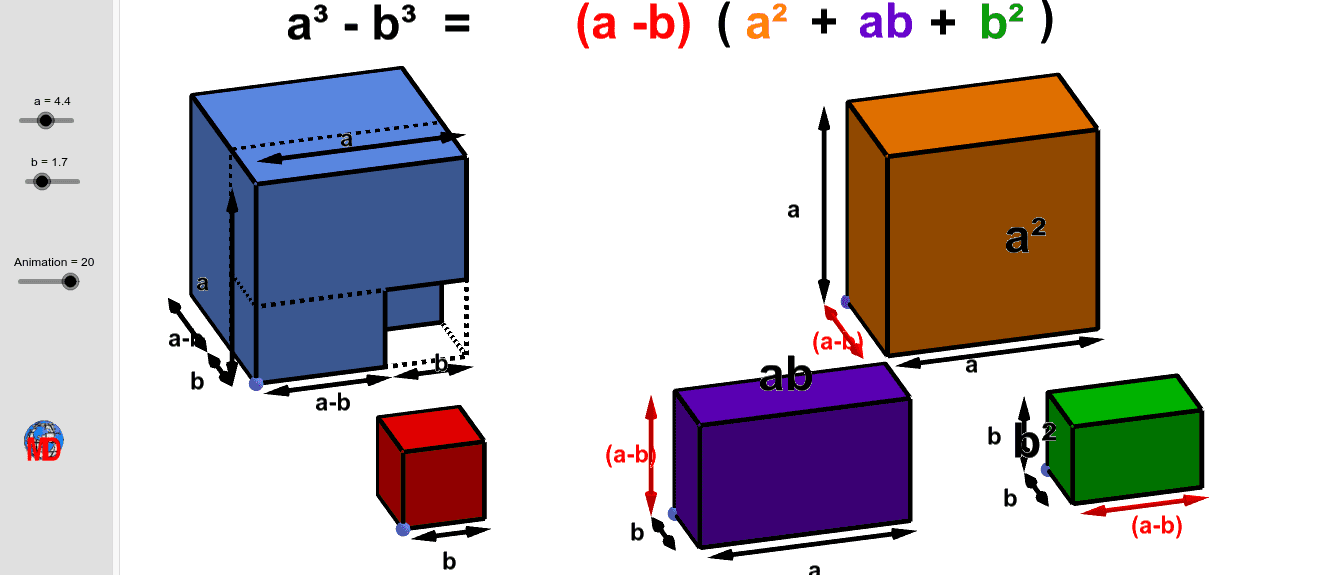
Proof Without Words Difference A 3 B 3 Geogebra

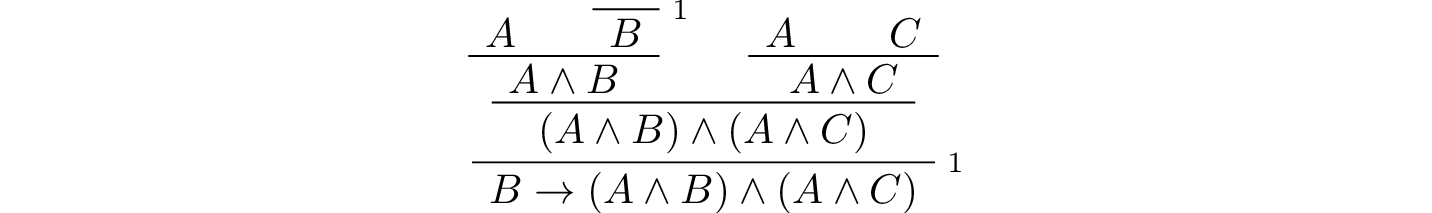
3 Natural Deduction For Propositional Logic Logic And Proof 3 18 4 Documentation

Answered Question 17 Consider This Proof Bartleby

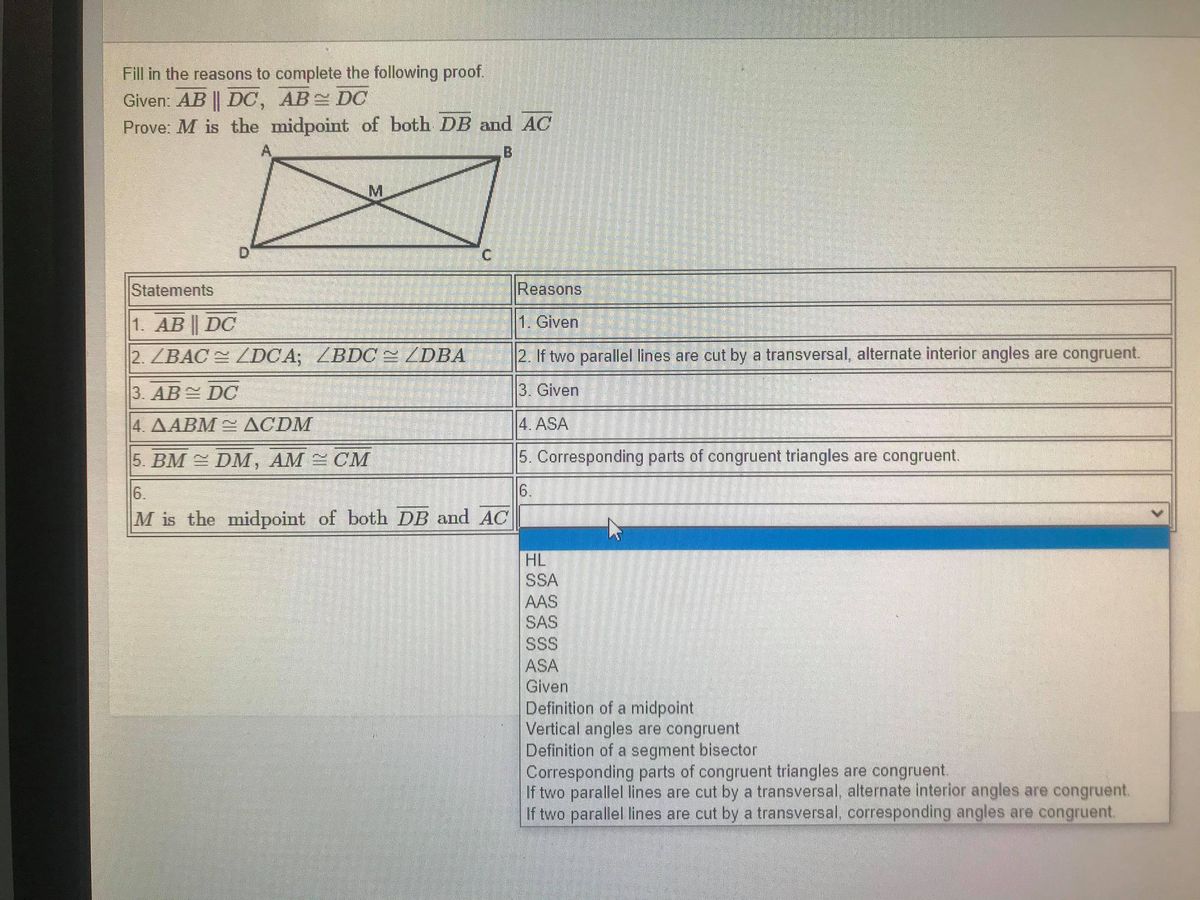
Answered Fill In The Reasons To Complete The Bartleby

Answered Complete The Proof By Giving The Bartleby

How To Prove That Ab T B Ta T Mathematics Stack Exchange

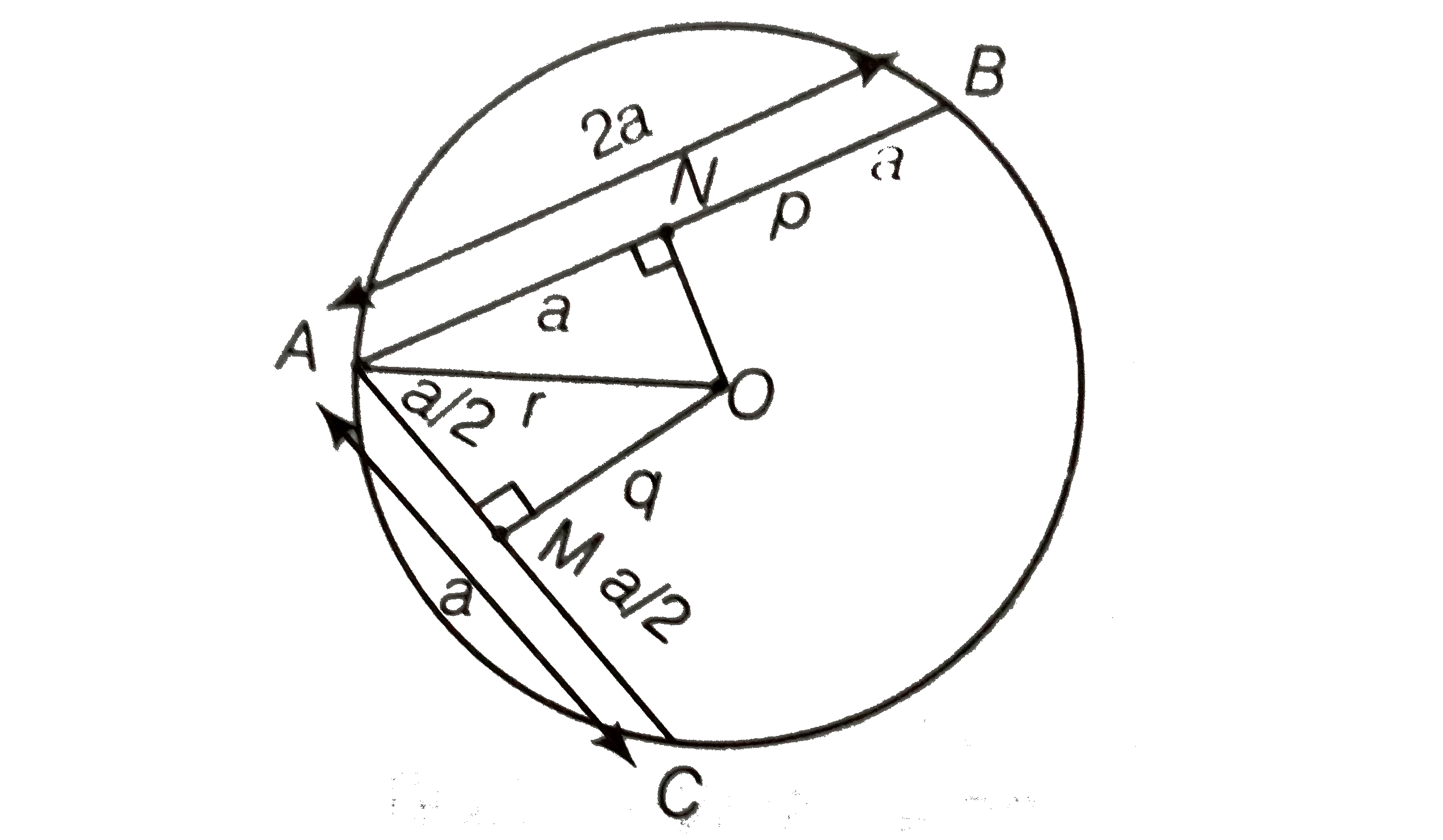
Ab And Ac Are Two Chords Of A Circle Of Radius R Such That Ab 2ac

Solved 3 Finish The Proof Of Theorem 45 If A Be R Then Chegg Com

Q Tbn And9gcrsvuubea2fyxbqdbdryxieweephs6lq6mbtcip97hxwvgag Ap Usqp Cau

Worksheet 2 6 Segment And Angle Proofs Pdf Segment And Angle Proofs Name Complete Each Proof D 1 Given A B And C Are Collinear Ab Prove Course Hero

A B 3 Geometrical Proof Youtube

Http Pehs Psd2 Org Documents Tfrey Pdf

View Question Help With Proof

How Should I Prove A B 3 A 3 3ab A B B 3 Model Or Figure Mathematics Stack Exchange

Given 1 4 2 3 Prove Ab Cd Which Of The Following Triangle Congruence Theorems Would Be Used Brainly Com

Www Edwardburkard Com Teaching 2 f18 Homework 4 solution Pdf

Yismxplusc Geometric Proof Of The Cubic Formula A B 3

Illustrations Of Formulas

When We Have Two Line Segments Ab And Cd What Does Ab Cd Mean Mathematics Stack Exchange

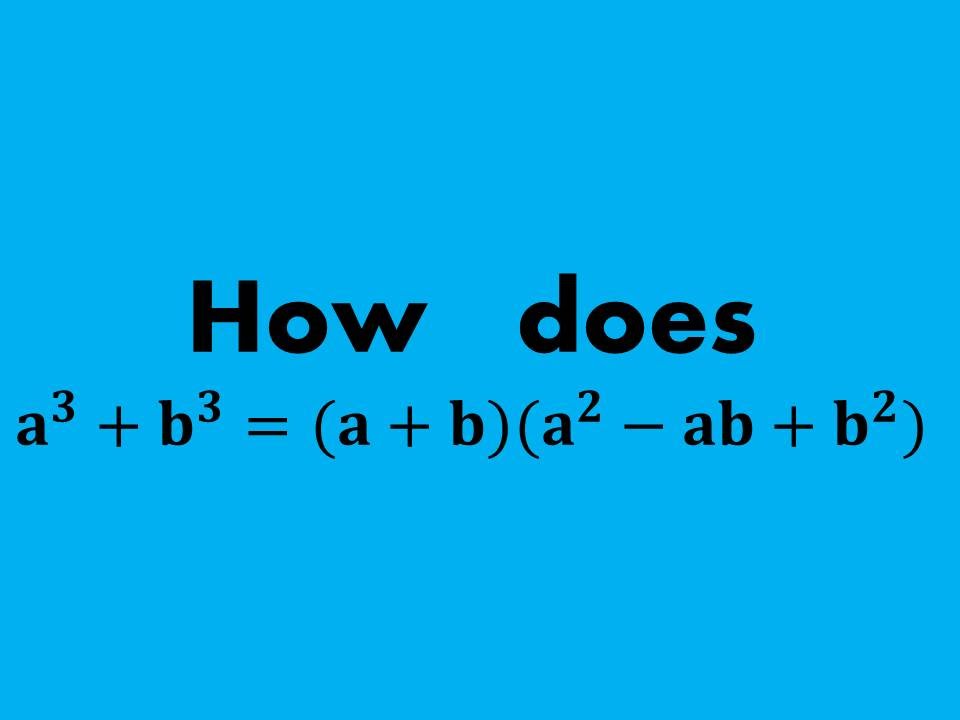
Proof How To Prove The Sum Of Two Cubes A 3 B 3 A B A 2 Ab B 2 Youtube

Mrwadeturner Segment Proofs

Www Math Uh Edu Ott Teaching Fa14 3325 Docs M3325 F14 V1 Pdf

Pythagorean Theorem Wikipedia

Http Www Math Drexel Edu Tolya Gcd Pdf

What Is The Formula Of Math A 3 B 3 Math Quora

Q Tbn And9gcsxj6nch9jkvcgw2jprateqxk Fehjaprpo Txh0pvbjcp 2po Usqp Cau

A Conjecture And The Flowchart Proof Used To Prove The Conjecture Are Shown Given Ab Xcprove M 1 Brainly Com

What Is The Correct Formula Of Math A B 3 Math Quora

Incoming Term: (a+b)^3 proof, (a+b+c)^3 proof, (a+b)^3 formula proof, (a+b)^3 geometric proof, (a+b+c)^3 formula proof, a^3+b^3+c^3-3abc proof,